Psych Icc Missing Try Again With Na omit or Set Missing False and Proceed at Your Own Risk

If y'all think my writing virtually statistics is articulate below, consider my educatee-centered, applied and concise Step-by-Pace Introduction to Statistics for Concern for your undergraduate classes, available at present from SAGE. Social scientists of all sorts will capeesh the ordinary, approachable linguistic communication and practical value – each chapter starts with and discusses a immature minor business organisation possessor facing a problem solvable with statistics, a trouble solved by the end of the affiliate with the statistical kung-fu gained.

---

This article has been published in the Winnower. Yous can cite it as:
Landers, R.N. (2015). Computing intraclass correlations (ICC) as estimates of interrater reliability in SPSS. The Winnower 2:e143518.81744. DOI: x.15200/winn.143518.81744

You can also download the published version as a PDF past clicking here.

---

Recently, a colleague of mine asked for some advice on how to compute interrater reliability for a coding job, and I discovered that at that place aren't many resources online written in an easy-to-empathize format – virtually either ane) go in depth well-nigh formulas and computation or 2) go in depth virtually SPSS without giving many specific reasons for why you'd make several of import decisions.  The primary resource available is a 1979 newspaper past Shrout and Fleiss1, which is quite dense.   So I am taking a stab at providing a comprehensive merely easier-to-empathize resource.

Reliability, generally, is the proportion of "existent" information almost a construct of interest captured by your measurement of it.  For example, if someone reported the reliability of their mensurate was .viii, you could conclude that eighty% of the variability in the scores captured by that measure represented the construct, and 20% represented random variation.  The more uniform your measurement, the college reliability will be.

In the social sciences, we oftentimes have inquiry participants consummate surveys, in which case you don't demand ICCs – y'all would more than typically use coefficient alpha.  But when yous accept research participants provide something about themselves from which you lot need to extract information, your measurement becomes what you get from that extraction.  For instance, in ane of my lab's current studies, we are collecting copies of Facebook profiles from enquiry participants, after which a team of lab assistants looks them over and makes ratings based upon their content.  This process is called coding.  Because the research assistants are creating the information, their ratings are my scale – non the original information.  Which means they 1) make mistakes and 2) vary in their ability to make those ratings.  An estimate of interrater reliability volition tell me what proportion of their ratings is "existent", i.e. represents an underlying construct (or potentially a combination of constructs – in that location is no fashion to know from reliability alone – all you tin can conclude is that you lot are measuring something consistently).

An intraclass correlation (ICC) can exist a useful estimate of inter-rater reliability on quantitative data because it is highly flexible.  A Pearson correlation can exist a valid calculator of interrater reliability, simply only when you have meaningful pairings between two and but 2 raters.  What if y'all take more?  What if your raters differ by ratee?  This is where ICC comes in (note that if yous have qualitative data, east.k. categorical data or ranks, you would not use ICC).

Unfortunately, this flexibility makes ICC a piffling more complicated than many estimators of reliability.  While you can ofttimes just throw items into SPSS to compute a coefficient blastoff on a calibration measure, there are several additional questions 1 must ask when computing an ICC, and one restriction. The restriction is straightforward: you must have the aforementioned number of ratings for every instance rated. The questions are more complicated, and their answers are based upon how y'all identified your raters, and what you ultimately want to do with your reliability gauge. Here are the first 2 questions:

1. Do you accept consistent raters for all ratees?  For example, do the exact same eight raters make ratings on every ratee?
2. Practice you have a sample or population of raters?

If your answer to Question 1 is no, yous need ICC(ane).  In SPSS, this is called "I-Fashion Random."  In coding tasks, this is uncommon, since you can typically control the number of raters fairly carefully.  It is well-nigh useful with massively large coding tasks.  For instance, if you lot had 2000 ratings to brand, you might assign your 10 research assistants to make 400 ratings each – each research assistant makes ratings on two ratees (you always have 2 ratings per case), just you counterbalance them so that a random ii raters make ratings on each subject.  It'due south called "One-Way Random" because 1) it makes no endeavor to uncrease the effects of the rater and ratee (i.due east. one effect) and 2) information technology assumes these ratings are randomly fatigued from a larger populations (i.e. a random effects model).  ICC(1) volition always be the smallest of the ICCs.

If your reply to Question 1 is yes and your answer to Question 2 is "sample", yous need ICC(2).  In SPSS, this is called "2-Style Random."  Unlike ICC(i), this ICC assumes that the variance of the raters is only adding dissonance to the estimate of the ratees, and that mean rater error = 0.  Or in other words, while a particular rater might rate Ratee one high and Ratee 2 low, it should all even out across many raters.  Similar ICC(1), it assumes a random effects model for raters, but it explicitly models this effect – you tin can sort of retrieve of it similar "controlling for rater effects" when producing an estimate of reliability.  If you have the same raters for each case, this is mostly the model to go with.  This will ever be larger than ICC(1) and is represented in SPSS as "2-Manner Random" because ane) it models both an effect of rater and of ratee (i.eastward. two effects) and 2) assumes both are fatigued randomly from larger populations (i.e. a random effects model).

If your answer to Question ane is yes and your answer to Question 2 is "population", yous need ICC(iii).  In SPSS, this is called "Two-Way Mixed."  This ICC makes the same assumptions every bit ICC(2), merely instead of treating rater effects equally random, it treats them as fixed.  This ways that the raters in your chore are the simply raters anyone would exist interested in.  This is uncommon in coding, considering theoretically your research assistants are only a few of an unlimited number of people that could make these ratings.  This means ICC(3) will also always be larger than ICC(1) and typically larger than ICC(ii), and is represented in SPSS every bit "Two-Way Mixed" because 1) it models both an outcome of rater and of ratee (i.e. ii effects) and 2) assumes a random event of ratee but a fixed upshot of rater (i.east. a mixed effects model).

Afterwards you've adamant which kind of ICC y'all demand, there is a 2nd decision to be made: are you interested in the reliability of a single rater, or of their mean?  If you're coding for research, you're probably going to apply the mean rating.  If you lot're coding to determine how accurate a single person would exist if they fabricated the ratings on their own, y'all're interested in the reliability of a unmarried rater.  For example, in our Facebook study, we want to know both.  First, we might inquire "what is the reliability of our ratings?"  Second, nosotros might ask "if i person were to make these judgments from a Facebook profile, how accurate would that person be?"  We add together ",grand" to the ICC rating when looking at means, or ",i" when looking at the reliability of unmarried raters.  For example, if you computed an ICC(2) with viii raters, you'd be calculating ICC(ii,8).  If you computed an ICC(i) with the same 16 raters for every case merely were interested in a single rater, you'd nevertheless be computing ICC(two,one). For ICC(#,ane), a large number of raters will produce a narrower confidence interval around your reliability guess than a small-scale number of raters, which is why y'all'd yet want a large number of raters, if possible, when estimating ICC(#,1).

Afterward you've determined which specificity yous need, the third decision is to figure out whether you lot need a measure of absolute agreement or consistency.  If you've studied correlation, you're probably already familiar with this concept: if two variables are perfectly consistent, they don't necessarily agree.  For example, consider Variable one with values 1, 2, 3 and Variable 2 with values 7, 8, 9.  Even though these scores are very different, the correlation between them is 1 – and then they are highly consequent simply don't agree.  If using a mean [ICC(#, 1000)], consistency is typically fine, especially for coding tasks, as mean differences between raters won't touch on subsequent analyses on that information.  But if y'all are interested in determining the reliability for a single individual, you probably want to know how well that score volition assess the real value.

One time you lot know what kind of ICC you want, it's pretty easy in SPSS.  First, create a dataset with columns representing raters (e.g. if you had 8 raters, you'd have 8 columns) and rows representing cases.  You'll need a complete dataset for each variable you are interested in.  So if y'all wanted to assess the reliability for viii raters on 50 cases across 10 variables being rated, y'all'd accept 10 datasets containing 8 columns and 50 rows (400 cases per dataset, 4000 total points of data).

A special note for those of you using surveys: if yous're interested in the inter-rater reliability of a calibration mean, compute ICC on that scale mean – non the private items. For example, if you have a ten-item unidimensional calibration, calculate the calibration mean for each of your rater/target combinations offset (i.due east. one hateful score per rater per ratee), and then apply that scale mean as the target of your ciphering of ICC. Don't worry most the inter-rater reliability of the individual items unless you are doing so as part of a scale evolution process, i.e. yous are assessing calibration reliability in a pilot sample in club to cut some items from your terminal scale, which you lot will afterward cross-validate in a 2nd sample.

In each dataset, you and so need to open the Analyze menu, select Calibration, and click on Reliability Analysis.  Move all of your rater variables to the right for analysis. Click Statistics and bank check Intraclass correlation coefficient at the lesser.  Specify your model (One-Style Random, Two-Way Random, or Two-Way Mixed) and type (Consistency or Absolute Agreement).  Click Continue and OK.  Yous should end upwardly with something like this:

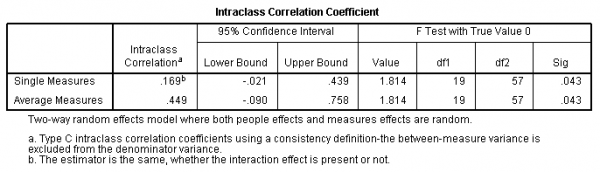
Results of a Two-Way Random Consistency ICC Calculation in SPSS

In this example, I computed an ICC(two) with 4 raters beyond xx ratees.  You can notice the ICC(2,i) in the first line – ICC(2,ane) = .169.  That means ICC(2, 1000), which in this example is ICC(2, four) = .449.  Therefore, 44.9% of the variance in the mean of these raters is "real".

So here'due south the summary of this whole procedure:

1. Make up one's mind which category of ICC you demand.
   1. Determine if you have consequent raters beyond all ratees (e.g. always 3 raters, and ever the aforementioned 3 raters).  If not, apply ICC(1), which is "One-manner Random" in SPSS.
   2. Determine if yous have a population of raters.  If yes, use ICC(3), which is "Two-Way Mixed" in SPSS.
   3. If you lot didn't utilize ICC(ane) or ICC(3), you need ICC(2), which assumes a sample of raters, and is "Two-Way Random" in SPSS.
2. Determine which value y'all volition ultimately use.
   1. If a unmarried individual, you want ICC(#,1), which is "Single Measure" in SPSS.
   2. If the mean, you desire ICC(#,k), which is "Boilerplate Measures" in SPSS.
3. Decide which set of values you ultimately want the reliability for.
   1. If you want to utilize the subsequent values for other analyses, you probably desire to assess consistency.
   2. If you want to know the reliability of individual scores, y'all probably desire to assess absolute agreement.
4. Run the analysis in SPSS.
   1. Analyze>Scale>Reliability Analysis.
   2. Select Statistics.
   3. Check "Intraclass correlation coefficient".
   4. Make choices as you decided to a higher place.
   5. Click Continue.
   6. Click OK.
   7. Interpret output.

1. Shrout, P., & Fleiss, J. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86 (2), 420-428 DOI: 10.1037/0033-2909.86.2.420 [↩]

williamsammed1960.blogspot.com

Source: https://neoacademic.com/2011/11/16/computing-intraclass-correlations-icc-as-estimates-of-interrater-reliability-in-spss/

Share this post